概率密度函数之一。彭尼帕克(Pennypacker,1980)将其引入植病流行学中病害季节性流行动态的研究,其微分形式为:
dX/dt=c/b(t-a/b)(c-1)exp[-(t-a)/b]c
积分形式可写成:Xt=1-exp{-(t-a)/b〕c}
(b>0,c>0,t>a)
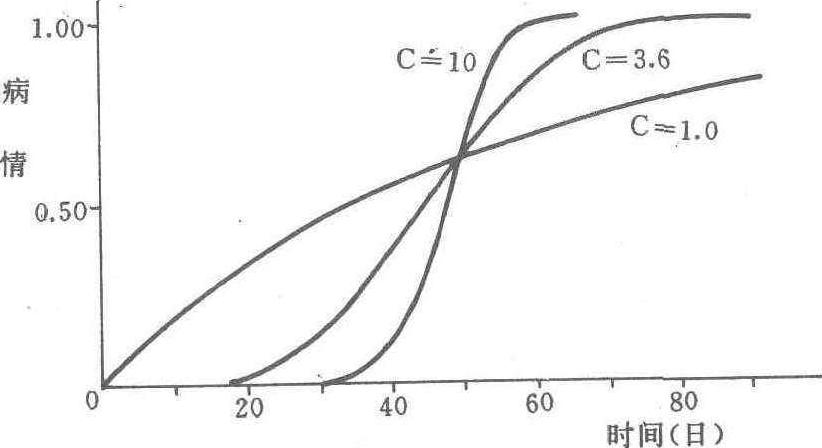
式中 Xt为时间t时的病情百分率;a为位置参数,决定病害始发期;b为比率参数,决定流行速度;c为流行曲线的形状参数,决定流行的先后速度的相对快慢。由于方程有三个参数,其种种组合可描述多种形式的流行曲线,因此也称弹性模型(flexible model)。当c=1时,韦布尔方程可代替指数模型用来描述单年病害流行。当c=3.6时可代替逻辑斯蒂模型用于描述单年流行病害的流行。式中的a为病害数量开始增长的日期。因 ......
上一篇: 微梯弗利亚效应
下一篇: 魏景超