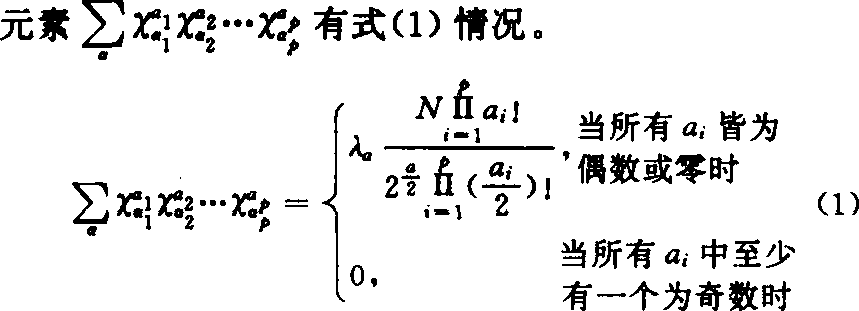
具有旋转性统计性质的回归设计。在编码值因子空间内与中心点等距的同一球面上各点的预测值方差都相等称为旋转性。旋转性减少了回归方程寻优的误差干扰,是一项重要的统计性质。二次正交回归设计不具有旋转性,预测值间的互比较为困难,旋转设计改善了这些不足。p元d次旋转设计的信息矩阵A是Cdp+d阶对称方阵。A中
式(1)中 指数a为各试验因素的次数,a1、a2、…ap为非负整数,N为试验方案的处理组合数,λa为待定参数,其下标为偶数,但λ0=1,式(1)称为旋转性条件。
应用最广的是p元二次旋转设计,其回归模型为:
旋转设计也是组合设计,N个处理分为三个部分:
N=mc+2p+m0 (3)
它们分布在三个半径 ......
上一篇: 形态诊断
下一篇: 雅戈金,Б.А.